Ny analysefunksjonalitet: Weibull

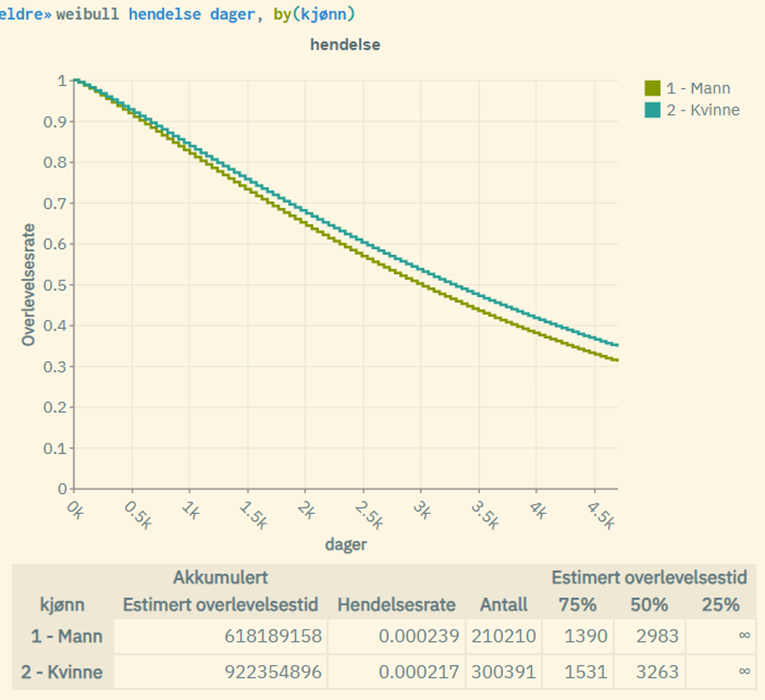
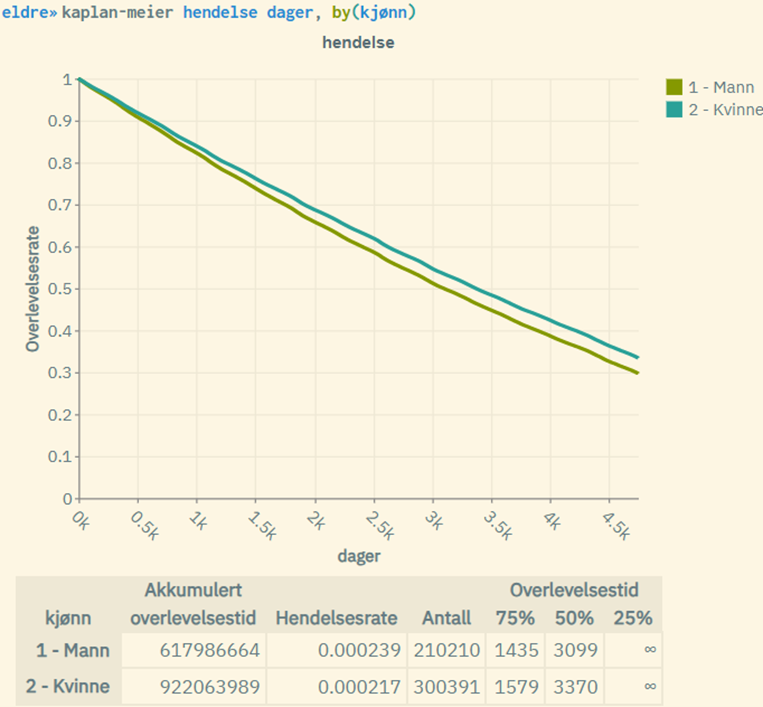
Weibull er en variant av overlevelsesanalyse som kan sammenliknes med Kaplan-Meier. Begge fremstiller overlevelsesrater målt over tid. Men der Kaplan-Meier viser de observerte endringer, presenterer Weibull resultatet av en parametrisk estimering. Weibull-grafene får dermed en mer glatt form sammenliknet med de typiske trappetrinn-grafene til Kaplan-Meier.

Weibull-modellen antar at overlevelsesdataene følger en spesifikk statistisk fordeling – Weibull-fordelingen. Modellen bruker matematiske parametere (som formparameteren β og skalaparameteren λ) for å definere hele fordelingen. Når disse parameterne er estimert fra dataene, brukes de til å generere en glatt, kontinuerlig overlevelseskurve som er en «beste tilpasning» til dataene. Den glatter ut dataene, noe som fører til en mer anonymisert visning (i forhold til Kaplan-Meier). Kaplan-Meier viser derimot de observerte hendelsene: Hver gang en hendelse inntreffer, faller overlevelseskurven et trinn. Fordi den kun bruker de observerte hendelsene, reflekterer grafen nøyaktig de observerte dataene uten å glatte ut eller interpolere mellom punktene.

Tilrettelegging av data

Forutsetningen for å kunne bruke kommandoen weibull er at datasettet ditt må være tilrettelagt for overlevelsesanalyse. Dette gjøres på samme måte som for kaplan-meier:

En ferdig definert måleperiode
En klar definisjon av hvilken hendelse man vil estimere sannsynligheten for
Datasettet må inneholde følgende variabler:
- Tid (f.eks. antall dager fra et felles starttidspunkt)
- Hendelse (0/1)

Klikk her for å vite mer om hvordan dette gjøres i praksis.

Forskjeller i resultater mellom Weibull og Kaplan-Meier

Jo mer detaljerte målinger man benytter, jo mindre forskjell blir det mellom resulatene til Kaplan-Meier (måler faktiske rater) og Weibull (estimerte rater beregnet fra en parametrisk modell). Man styrer dette gjennom å justere på antall individer som er med i analysen, og hvor detaljert tidsskalaen er (tidsgranularitet). Om det er mange enheter med i analysen, og tidsgranulariteten er høy, vil det i praksis være små forskjeller mellom resultatene til henholdsvis Kaplan-Meier og Weibull.

Her er resultatene knyttet til et case der man måler dødsraten til alle personer over 70 år. Granularitet er dager, mens antall enheter (individer) utgjør ca. 510 000. Forskjellene blir da ganske små, og de estimerte hendelsesratene til Weibull blir helt identiske med de faktiske ratene som Kaplan-Meier rapporterer:

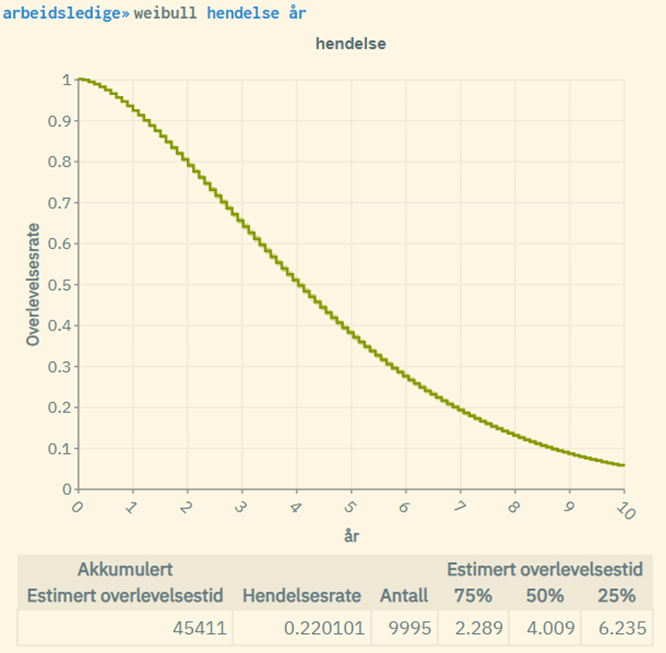
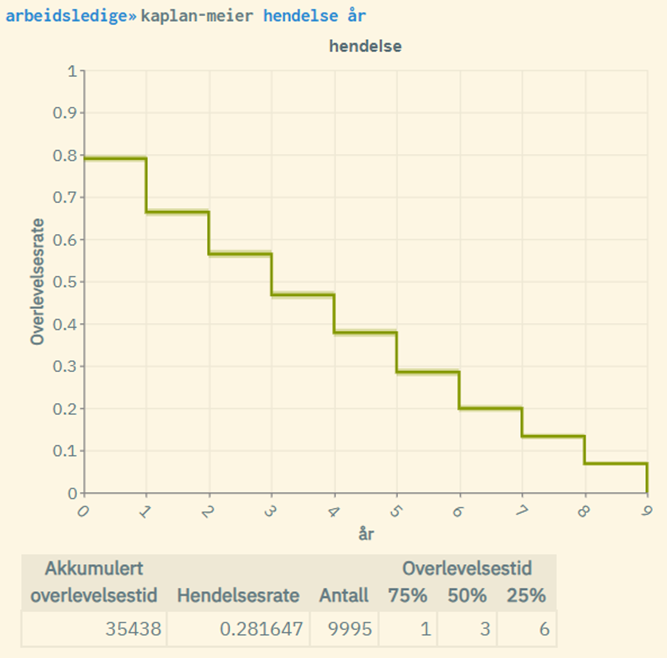
Her er et annet case der man ser på et tilfeldig utvalg på 10 000 personer (resultatet under grafen viser 9995 grunnet standard støylegging på +/- 5) som blir arbeidsledig i perioden 2010-2019, og måler ledighetsraten over tid (når man først blir ledig). Granularitet er her år. Antallet enheter (individer) er dessuten ganske lavt. Her ser vi at forskjellen i resultatene er større, med hendelsesrater på hhv. 0.22 og 0.28:

Om man øker granulariteten til dager i stedet for år, blir forskjellen mindre, og hendelsesratene blir tilnærmet identiske:

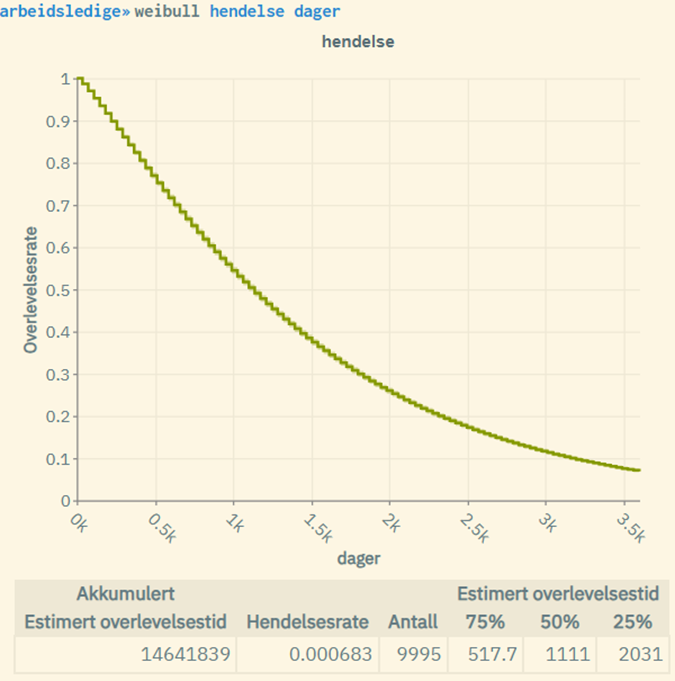
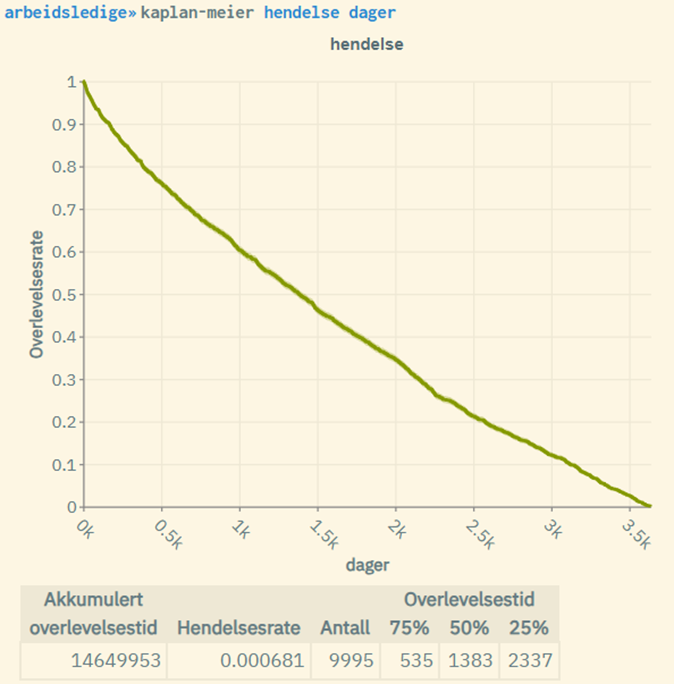
Eksempel der man estimerer separate overlevelsesrater for tre delgrupper basert på en tredelt aldersinndeling:

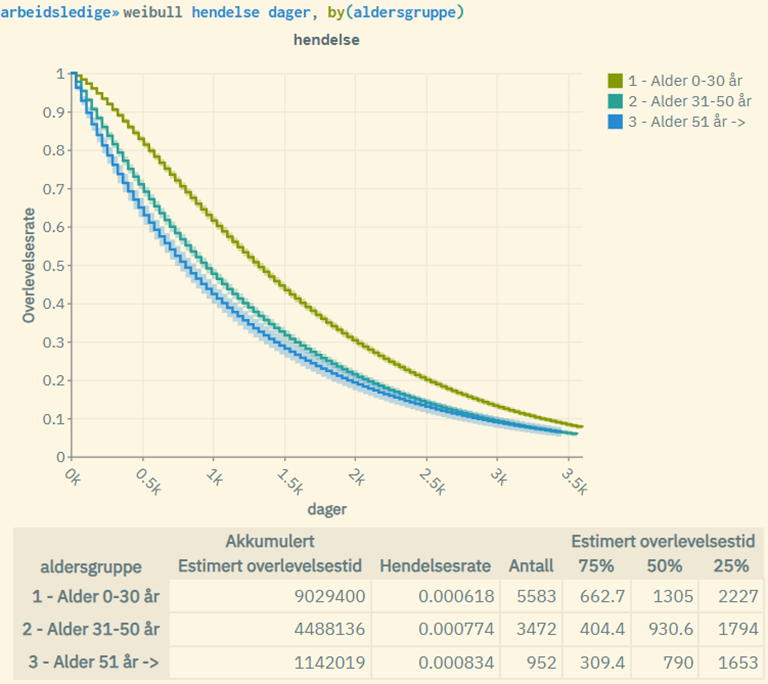
Tolkning av resultatene

Overlevelseskurvene viser hvor mange som er igjen i utvalget over tid. De synker alltid over tid fordi de baseres på den kumulative sannsynligheten for å overleve. Hver gang en hendelse (f.eks. et dødsfall) inntreffer, faller sannsynligheten for overlevelse for gruppen. Den kan ikke stige. Den vil enten forbli flat (når ingen hendelser skjer) eller falle.
De skraverte områdene representerer standard log-log 5% konfidensintervall tilknyttet overlevelsesraten. Disse vil være mindre synlig ved store populasjoner.
«Akkumulert (estimert) overlevelsestid»: Summen av tid målt over alle enheter i populasjonen (innen hver delgruppe der dette er aktuelt)
«Hendelsesrate»: Antall hendelser inntruffet (antall enheter med hendelse = 1) dividert med «akkumulert overlevelsestid».
«Antall»: Antall enheter (for hver av delgruppene)
«75%»: Tid målt der hvor overlevelsesraten = 0.75 (for hver av delgruppene)
«50%»: Tid målt der hvor overlevelsesraten = 0.5 (for hver av delgruppene). Også kalt «median overlevelsestid»
«25%»: Tid målt der hvor overlevelsesraten = 0.25 (for hver av delgruppene)

Grafisk fremstilling og personvern

Kaplan-Meier-grafer fremstiller faktiske endringer i overlevelsesrater (og ikke estimerte). Det har i enkelte situasjoner vist seg å være vanskelig å beskytte personvernet optimalt uten å støylegge endringene i overlevelsesratene som tegnes i grafen. Men det har også vist seg vanskelig å støylegge disse endringene uten å introdusere for stor usikkerhet med tanke på tolkning av Kaplan-Meier-grafene, fordi støyleggingen har en kumulativ effekt over tidsperioden.

Vi har derfor valgt å fjerne den grafiske fremstillingen for kommandoen kaplan-meier. De mindre detaljerte hovedtallene under grafen beholdes, og kan brukes som før.

For kommandoen weibull baserer de genererte overlevelsesgrafene seg på estimerte/predikerte overlevelsesrater (med utgangspunkt i de faktiske observasjoner), og personvernutfordringene er vesentlig mindre.

Om det viktigste for deg er å lage grafiske fremstillinger av overlevelsesrater, anbefaler vi derfor å benytte kommandoen weibull. Merk at hovedtallene hentes ut fra den estimerte grafen, og at tallene derfor har en viss unøyaktighet i forhold til det kaplan-meier rapporterer. Om korrekte tall er det viktigste, anbefaler vi å bruke kaplan-meier som fortsatt produserer en tabell. De to kommandoene kan også kombineres. Men da må det tas forbehold om at weibull-grafene viser den trendmessige utviklingen, og ikke de faktiske/ observerte endringer.